Há um tempo tenho feito alguns textos como base para elaborar publicações de divulgação científica no meu Instagram e Twitter. Resolvi então transformar esses roteiros em postagens para blogs. Hoje eu venho trazer aqui uma forma de ver o mundo, e que todas as pessoas deviam saber, trazida pelo Teorema de Bayes. Carreguem isso para a vida de vocês.
Sem muita enrolação o Teorema de Bayes diz que:
“A probabilidade de que uma hipótese H esteja correta, dada uma nova evidência E, é igual à probabilidade a priori, multiplicada pela probabilidade de se observar a evidência, caso a hipótese seja verdadeira, dividido pela soma da probabilidade a priori vezes a probabilidade de se observar a evidência, caso a hipótese seja verdadeira com a probabilidade a priori de que a hipótese seja falsa multiplicada pela probabilidade de se observar a evidência, caso a hipótese verdadeira seja falsa.”
Parece complicado? Isso é uma forma de traduzir a seguinte equação:
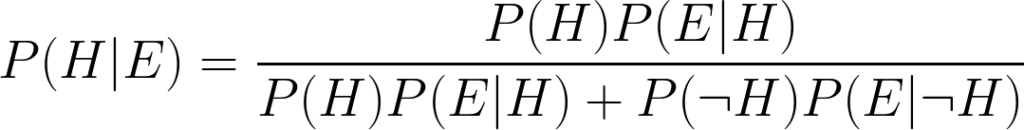
Aqui,
- P(H|E) é a probabilidade de que a hipótese seja verdadeira, dada uma evidência;
- P(H) é a probabilidade de que a hipótese fosse verdadeira ANTES de se ver a evidência;
- P(E|H) é a probabilidade de se ver a evidência, caso a hipótese seja verdadeira;
- P(¬H) é a probabilidade de que a hipótese fosse falsa ANTES de se ver a evidência;
- e por fim, P(E|¬H) é a probabilidade de se ver a evidência, caso a hipótese seja falsa.
De maneira simplificada, o Teorema de Bayes nos informa que uma nova evidência apenas atualiza uma probabilidade anterior, e que a nova probabilidade depende não apenas da evidência encontrada, mas sim da probabilidade anterior à evidência. Podemos traduzir isso da seguinte forma: O teorema nos diz que a crença que você tem em algo, após ver um evidência a favor ou contra este algo, dependa de o quão crente você era neste algo antes de ver a evidência. Ou seja, o teorema nos dá uma formulação matemática para descrever a atualização de crenças e opiniões em pessoas!
Na verdade, alguns historiadores defendem que foi nesse intuito que Thomas Bayes elaborou seu teorema no século XVIII (18). Thomas era um ministro presbiteriano na capela de Mount Sion, na Inglaterra. Em 1748, o filósofo David Hume argumentou que a probabilidade de que uma pessoa erroneamente acredite ter visto a ressurreição de cristo é muito maior do que a probabilidade de que o evento tenha de fato acontecido. E foi inspirado nesta lógica que Bayes tentou elaborar uma formulação matemática para este argumento, resultando nas bases de fundação do Teorema de Bayes.
Bayes nos trás uma visão matemática para o processo de formação de crenças e opiniões! Há debates em Psicologia a respeito de o quão bem a ideia do teorema é capaz de representar de fato o processo de mudança ou fortalecimento de crenças nas pessoas. Independentemente disso, é inegável que o teorema é uma boa forma de se observar o processo, ao menos de forma simplificada. Faremos aqui um caso de exemplo para fixar a ideia.
Imagine que duas pessoas testemunhem o mesmo evento, ambas veem uma luz no céu passando rapidamente e piscando. A diferença entre as pessoas é que uma delas é um entusiasta ufólogo, enquanto a outra é um cético. Vamos então utilizar o Teorema de Bayes para quantificar o quanto a crença das duas pessoas na existência de ETs é alterada frente a este evento. Para o nosso entusiasta, Fred, vamos supor que ele crê que a chance de que ETs existam é de 90%, portanto a probabilidade a priori de Fred para a hipótese à respeito da existência de ETs é P(H)₁ = 0,9. Enquanto isso, nossa cética Luisa já estima que a chance seja de 5%, assim P(H)₂ = 0,05.
Vamos considerar que, caso ETs existam, eles tentem tomar bastante cuidado para não serem vistos, e com isso, a chance de alguém ver uma nave voando pelo céu noturno é de apenas 5%. Enquanto, caso ETs não existam, a chance de se observar uma luz voando pelo céu (que possa ser um avião, ou um drone, por exemplo) é de 1%.
Assim, utilizando o teorema de Bayes, podemos calcular as crenças de Fred e Luisa, após avistarem este fenômeno, supondo que eles tenham uma certa noção dessas proporções mencionadas no parágrafo acima.

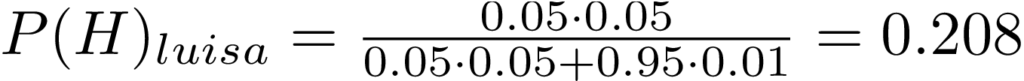
Pare pra ver esse resultado, ambas as pessoas viram o mesmo evento, mas uma delas agora está quase certa que ETs existem, enquanto outra ainda esta relativamente cética. O motivo para isso está na crença a priori P(H) de cada uma delas, era a única coisa diferente entre elas!
Podemos visualizar a forma como, de acordo com o teorema de Bayes, as crenças se atualizam quando veem novas evidências:
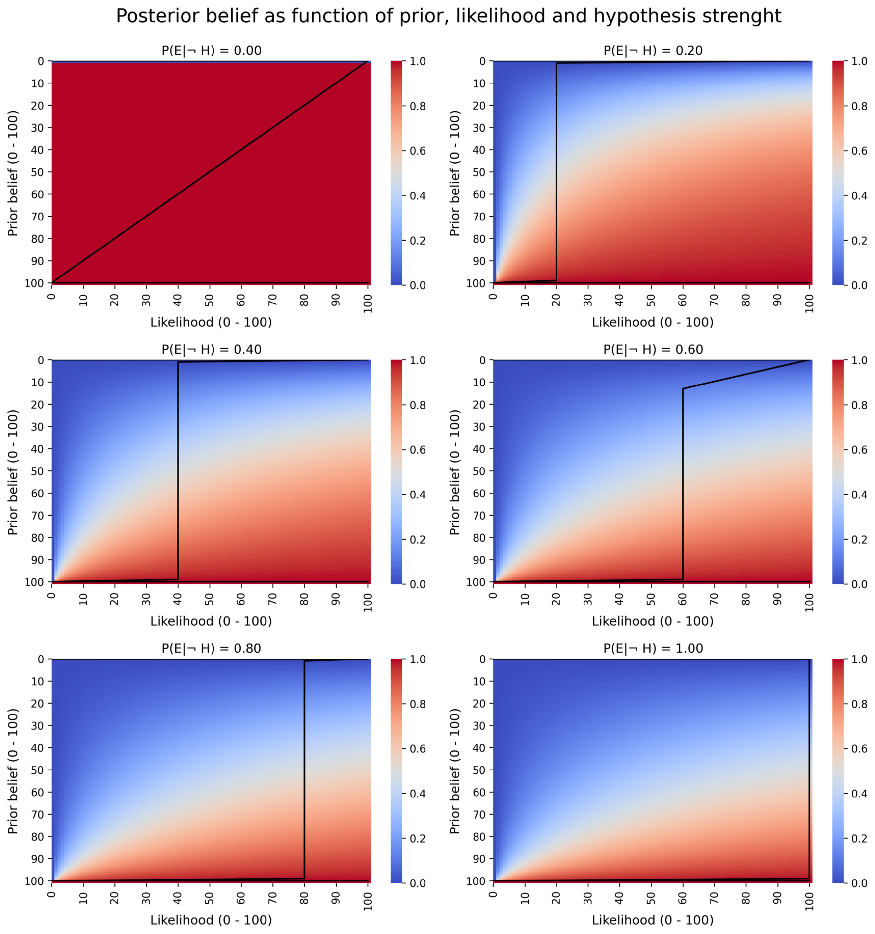
O que vemos aqui é um mapa de cores que representa a crença a posteriori (após ver uma evidência) de uma pessoa, em função da probabilidade de se observar a evidência, caso a hipótese esteja certa (likelihood) e a crença a priori. Cada um dos 6 gráficos é para valores diferentes de P(E|¬H). Vejam que, caso P(E|¬H) seja zero, a chance de se observar esta evidência caso a hipótese seja falsa é nula, e a crença a posteriori de todos os indivíduos é 100%, independente da crença a priori, exceto em um caso. Isso faz sentido, uma vez que é impossível se observar um fenômeno sem considerar uma hipótese, se este fenômeno for observado, a hipótese necessita necessariamente ser verdadeira, independente de o quanto se acreditava nela antes. O único caso em que a crença posterior não muda é quando a crença a priori é nula. Ou seja, se pessoas estão 100% convencidas de que uma hipótese é falsa, nenhuma evidência a favor muda a crença delas (note que a linha onde P(H)=0 continua azul em todos os 6 mapas de cores).
Além disso, as linhas pretas, que representam a combinação de P(H) e P(E|H) em que a crença posterior não muda, sempre está em cima da região onde P(E|H) = P(E|¬H). O que novamente faz sentido, se a chance de se observar um fenômeno é a mesma independente da hipótese ser verdadeira ou falsa, observar este fenômeno não muda nossa crença. A chance de você observar uma pessoa míope na rua, é a mesma caso o modelo padrão de partículas seja falso ou verdadeiro, logo, é natural que ninguém dê mais ou menos crédito ao modelo padrão toda vez que observa um míope na rua.
No último gráfico (direita inferior), note que P(E|¬H) = 1. Isso nos diz que, a chance de se observar um fenômeno é 100% caso a hipótese seja falsa. E naturalmente, se a nossa hipótese tem uma chance menor que 100% de se observar a evidência, descremos nela.
Por último, note que sempre que a crença a priori de um indivíduo é 100%, sua crença posterior continua 100%. Nada disso é novidade se você olhar a matemática do teorema, de fato, se P(H)=1, então P(¬H)=0 e o denominador e o numerador da equação são iguais, portanto P(H|E) = 1 sempre. Na prática, o que tiramos disso é: pessoas 100% convencidas de que algo é verdadeiro e pessoas 100% convencidas de que algo é falso não mudam sua crença independentemente da força da evidência apresentada. Há motivos psicológicos para essa resistência à mudar de opinião, conforme a crença das pessoas tende a um dos dois extremos. Um estudo avaliando a crença politica de pessoas encontrou que, quando apresentadas com evidências contra a crença delas, o cérebro possuía maior atividade em regiões relacionadas à reação contra ameaças. Isso indica que, uma vez que a crença de alguém está estabelecida fortemente, o cérebro interpreta afrontas a essa crença como afrontas contra a pessoa, não simplesmente como uma exposição à novas informações.
Apesar de que na realidade pessoas não possuem nas suas cabeças as probabilidades de cada fenômeno acontecer (e talvez essa seja a maior crítica a analogias com o Teorema de Bayes e crenças humanas), o Teorema de Bayes nos traz a intuição sobre como a crença de indivíduos muda, dependendo da força que elas atribuam à evidência e a de suas crenças anteriores. Essa forma de se visualizar o teorema tem uma profunda conexão com a forma como formamos opiniões. Primeiro, opiniões extremas mudarão com cada vez mais dificuldade, portanto, às vezes vale mais a pena se poupar do esforço do que trabalhar para adquirir uma evidência forte e apresentá-la, para no fim e crença não ter qualquer alteração. Segundo, nenhuma evidência deve ser analisada sozinha, sem considerar as hipóteses que se relacionam com ela.
Nas próximas vezes que duvidar de algum argumento, tenha em mente o Teorema de Bayes e se pergunte, se você não está convencido pois o argumento é fraco (ou a evidência é fraca), ou se sua crença a priori é que está dificultando sua decisão.
Para saber mais
Referências
Dezert, J., Tchamova, A., & Han, D. (2018, July). Total belief theorem and generalized Bayes’ theorem. In 2018 21st International Conference on Information Fusion (FUSION) (pp. 1040-1047). IEEE. 10.23919/ICIF.2018.8455351
French, S. (1980). Updating of belief in the light of someone else’s opinion. Journal of the Royal Statistical Society: Series A (General), 143(1), 43-48. https://doi.org/10.2307/2981768
McNamara, J. M., Green, R. F., & Olsson, O. (2006). Bayes’ theorem and its applications in animal behaviour. Oikos, 112(2), 243-251.https://doi.org/10.1111/j.0030-1299.2006.14228.x
Áudio do post
Em breve : )
Siga por e-mail e compartilhe nas redes sociais
Capa do post: Imagem elaborada pelo autor do texto.
Sobre o autor

Pedro Henrique Pinheiro Cintra. É mestrando em Física na UNICAMP e trabalha com detecção de neutrinos de supernova. Durante sua graduação em Física na UnB realizou pesquisas sobre modelos matemáticos epidemiológicos, espectroscopia ótica de microalgas e sobre percepção visual utilizando rastreamento ocular. Ama Legos, se fantasia de homem-aranha e divulga ciência no Twitter (@pedrocintra52).
Este texto foi originalmente publicado no Medium em 31/03/2021.
Termos de reprodução e divulgação do texto
Todos os textos publicados no eupercebo.unb.br podem ser reproduzidos na íntegra ou parcialmente por meios impressos e digitais, desde que não sofram alterações de conteúdo e que a fonte seja mencionada. Como referenciar este texto (normas da APA):
Cintra, P. H. P. (2021, 14 de abril). Teorema de Bayes: A matematização da crença. Eu Percebo. https://eupercebo.unb.br/2021/04/17/teorema-de-bayes-a-matematizacao-da-crenca

